Example of Algorithm Questions

Example of Algorithm Questions: Key Problems and Solutions for Coding Interviews

Algorithms form the backbone of computer programming and problem-solving. For those preparing for coding interviews or working on technical skills, understanding common algorithm questions is crucial. In this article, we’ll cover some of the most typical algorithm problems, breaking them down with solutions and concepts that are useful for both beginners and experienced coders.

1. What is an Algorithm?

Before diving into the examples, let’s briefly define an algorithm. An algorithm is a set of instructions designed to perform a specific task. In computer science, algorithms are often used to solve problems, from searching and sorting data to more complex operations like pathfinding or optimization. Understanding how to create efficient algorithms is essential to writing optimized and scalable code.

2. Common Types of Algorithm Questions

Algorithm questions in coding interviews typically fall into several key categories:

Sorting and Searching Algorithms
Dynamic Programming
Graph Algorithms
Greedy Algorithms
Recursion
Backtracking

Below, we’ll explore examples from these categories to give you a solid foundation for tackling coding challenges.

3. Example Algorithm Questions

a. Two Sum (Array & Hashing)

This is one of the most common algorithm questions in coding interviews. The problem statement is:

Problem: Given an array of integers nums and an integer target, return the indices of the two numbers that add up to the target. You may assume that each input would have exactly one solution.

Solution Approach:

A brute force solution would involve checking every pair of numbers in the array to see if they sum up to the target, which would take $O(n^2)$ time complexity. However, a more efficient solution involves using a hash map to store the complements of the elements we are iterating over, which reduces the complexity to $O (n)$ .

python

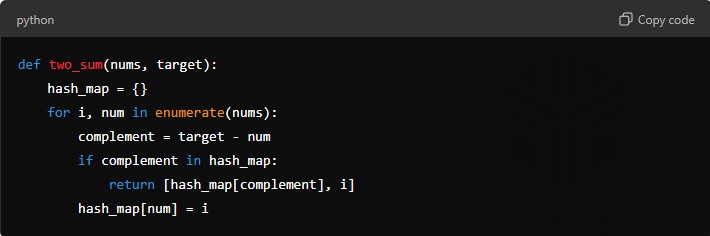
def two_sum(nums, target):

    hash_map = {}

    for i, num in enumerate(nums):

        complement = target - num

        if complement in hash_map:

            return [hash_map[complement], i]

        hash_map[num] = i

b. Merge Sort (Sorting Algorithm)

Merge Sort is a classic divide-and-conquer sorting algorithm with a time complexity of $\log n)$ . It works by recursively dividing the array into halves until each subarray contains only one element, then merging the sorted halves.

Problem: Given an array of unsorted integers, sort it using the merge sort algorithm.

Solution Approach:

python

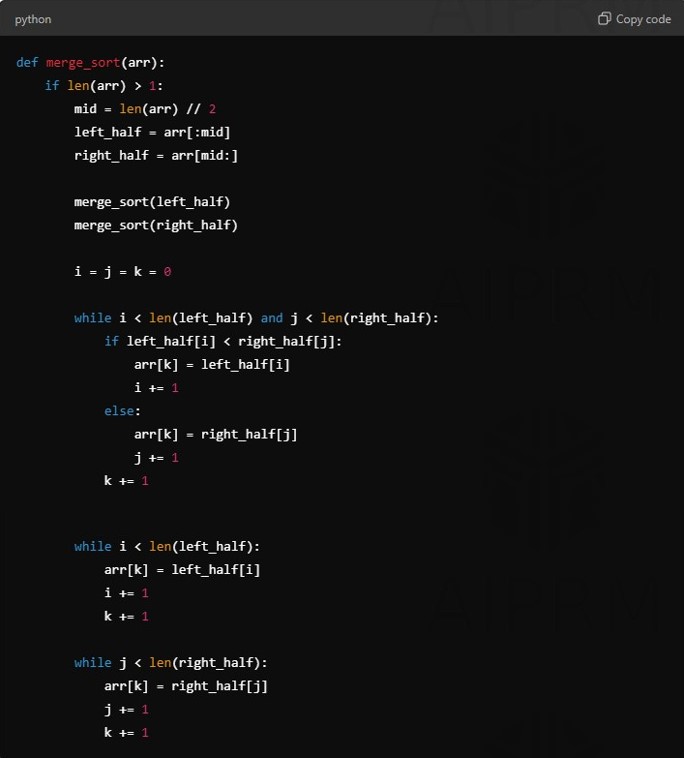
def merge_sort(arr):

    if len(arr) > 1:

        mid = len(arr) // 2

        left_half = arr[:mid]

        right_half = arr[mid:]






        merge_sort(left_half)

        merge_sort(right_half)
        i = j = k = 0






        while i < len(left_half) and j < len(right_half):

            if left_half[i] < right_half[j]:

                arr[k] = left_half[i]

                i += 1

            else:

                arr[k] = right_half[j]

                j += 1

            k += 1
        while i < len(left_half):

            arr[k] = left_half[i]

            i += 1

            k += 1

while j < len(right_half): arr[k] = right_half[j] j += 1 k += 1

Merge sort is often asked in interviews due to its stable sorting and optimal time complexity for large datasets.

c. Fibonacci Sequence (Dynamic Programming)

The Fibonacci sequence is a popular problem for teaching recursion and dynamic programming concepts. The problem is:

Problem: Write a function to calculate the nth Fibonacci number.

Recursive Solution (Inefficient):

python

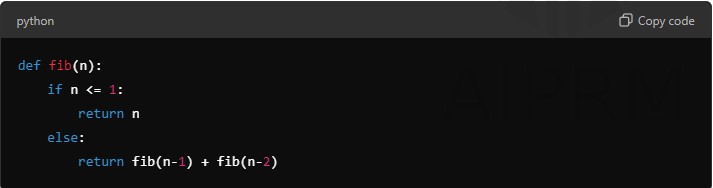
def fib(n):

    if n <= 1:

        return n

    else:

        return fib(n-1) + fib(n-2)

This recursive solution has an exponential time complexity, $O(2^n)$ , because it recalculates the same subproblems multiple times.

Dynamic Programming Solution (Efficient):

Using dynamic programming to store the results of subproblems reduces the time complexity to $O (n)$ .

python

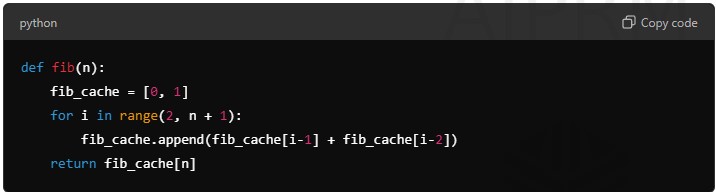
def fib(n):

    fib_cache = [0, 1]

    for i in range(2, n + 1):

        fib_cache.append(fib_cache[i-1] + fib_cache[i-2])

    return fib_cache[n]

4. Graph Algorithms

d. Depth-First Search (DFS) & Breadth-First Search (BFS)

Graph traversal algorithms such as DFS and BFS are essential tools for navigating graphs and trees. Both algorithms are often asked in interviews, especially for problems related to pathfinding and connectivity.

Problem: Given a graph, implement DFS and BFS to traverse all nodes.

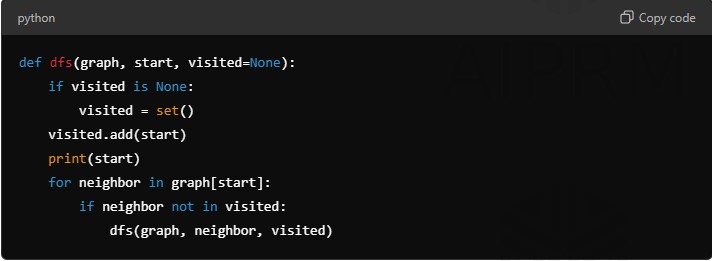
Depth-First Search (DFS):

python

def dfs(graph, start, visited=None):

if visited is None:

visited = set()

visited.add(start)

print(start)

for neighbor in graph[start]:

if neighbor not in visited:

dfs(graph, neighbor, visited)

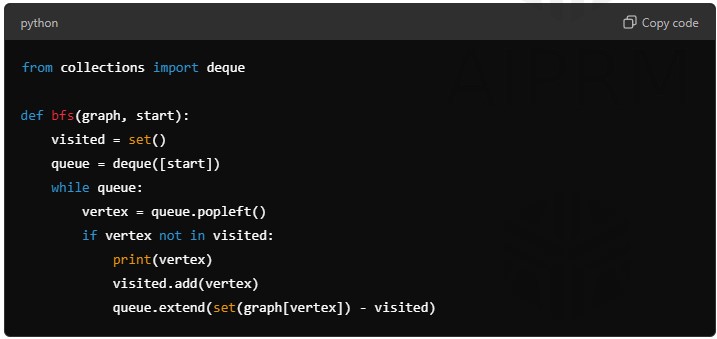
Breadth-First Search (BFS):

python

from collections import deque

def bfs(graph, start):
visited = set()
queue = deque([start])
while queue:
vertex = queue.popleft()
if vertex not in visited:
print(vertex)
visited.add(vertex)
queue.extend(set(graph[vertex]) – visited)

DFS explores as far as possible along each branch before backtracking, while BFS explores all neighbors at the present depth before moving on to nodes at the next depth level.

5. Greedy Algorithms

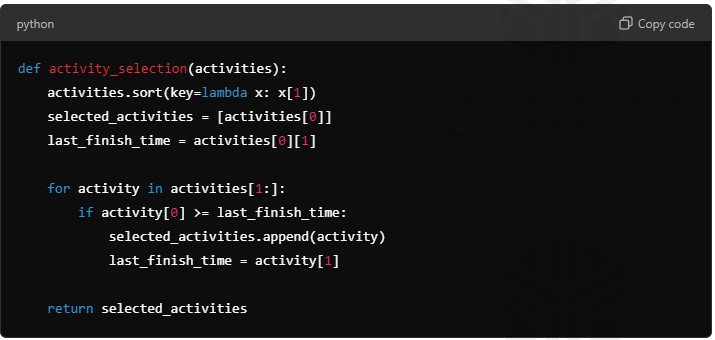
e. Activity Selection Problem (Greedy Algorithm)

The activity selection problem is a famous greedy algorithm problem. The objective is to select the maximum number of non-overlapping activities from a list of activities, where each activity has a start and end time.

Problem: Given a set of activities with start and end times, choose the maximum number of activities that don’t overlap.

Greedy Approach:

The key to solving this problem is to always select the activity that finishes the earliest, ensuring that there is as much room as possible for future activities.

python

def activity_selection(activities):

activities.sort(key=lambda x: x[1])

selected_activities = [activities[0]]

last_finish_time = activities[0][1]

for activity in activities[1:]:
if activity[0] >= last_finish_time:
selected_activities.append(activity)
last_finish_time = activity[1]return selected_activities

The time complexity of this solution is $\log n)$ due to the sorting step.

6. Recursion and Backtracking

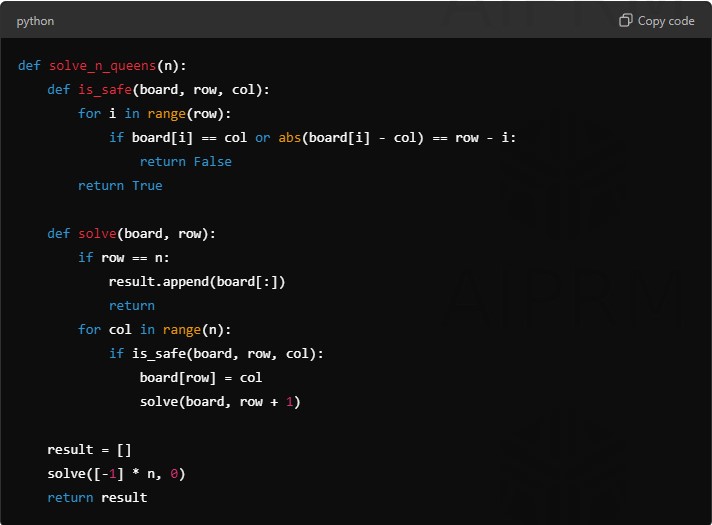
f. N-Queens Problem (Backtracking)

The N-Queens Problem is a classic example of a backtracking algorithm. The objective is to place N queens on an N×N chessboard so that no two queens threaten each other.

Problem: Place N queens on an N×N chessboard such that no two queens share the same row, column, or diagonal.

Backtracking Solution:

python

def solve_n_queens(n):

def is_safe(board, row, col):

for i in range(row):

if board[i] == col or abs(board[i] - col) == row - i:

return False

return True

def solve(board, row):
if row == n:
result.append(board[:])
return
for col in range(n):
if is_safe(board, row, col):
board[row] = col
solve(board, row + 1)result = []
solve([-1] * n, 0)
return result

Backtracking is a powerful technique for solving constraint satisfaction problems like this.

Conclusion

Mastering algorithm questions is essential for anyone preparing for technical interviews. By familiarizing yourself with common problems such as sorting, searching, dynamic programming, and graph traversal, you can build the confidence to solve even the most challenging algorithmic questions.

Consistent practice is the key to success, so take time to work through these examples, refine your problem-solving skills, and keep up with the latest algorithm trends in coding interviews.